|
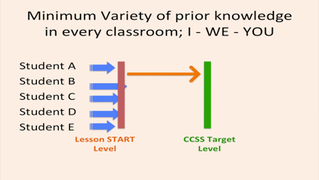
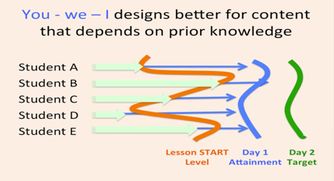
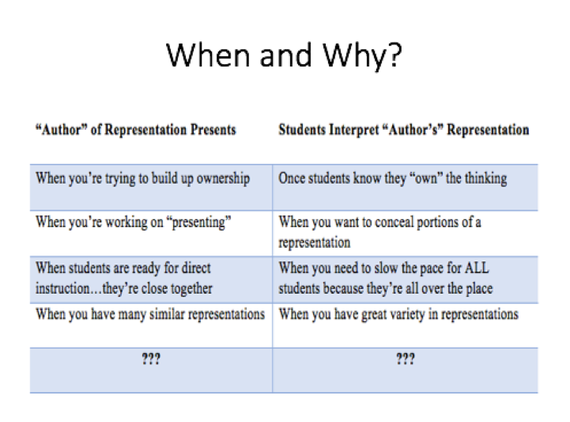
Could it be that the exhausting debate about whether reasoning, problem-solving and conceptual understanding need some serious attention in math education is near consensus? Do we have enough believers in our midst that we can move on from selling the product of a student-centered classroom and now move on to the “how”…while maintaining balance? After spending 2 days with some of the highest quality math education professionals in our nation, I'm posting my take-aways. It’d be an interesting survey to collect your “noticings” of these from this weekend’s CA Math Council – South. Blessed to get CMC started with my own session, Promoting Depth through Students’ Representations, we honed in on the intricacies of connecting representations. Using the premise proposed by CCSSM author Phil Daro, in Four Levels of Learning, teachers compared these 2 visuals. What is direct instruction good for...and when? Inspired by Dan’s talk on Deleting the Textbook, and through a killer Numberless Word Problem adapted from van de Walle that exposed the progression of thinking that leads to the “invert-and-multiply” algorithm for dividing fractions, teachers experienced the student end of the 5 Practices for Orchestrating Productive Discussions. However, no teacher presented their way of thinking. Rather teachers were asked to analyze different aspects of different representations, and tried to infer and interpret what the creator of that representation was thinking, and why. Hence, we took a deeper dive into examining what conditions should exist in the classroom that would help a teacher determine whether to have the student who created a representation “present” his or her way of thinking to the group, versus having the teacher displaying the representation and asking all students to engage in discourse about the features of that representation, BEFORE having the creator of the representation speak about it. Can you make the connection between the visuals above and this critical distinction to consider when connecting representations? Who should be talking and when? Can you please dig into the intricate decision-making when connecting students representations that move towards learning new and important mathematics? The current, and likely temporarily and incomplete, conclusion came as follows: I buzz over to Tim McCaffery’s session, who’s promoting the 5 Practices through engaging in a system of linear equations task, and exposing to a large group there is a difference between having students present, and asking others to interpret what that person was thinking...ideas we've examined together over the past few months.
Steve Leinwand once again lights up the room, but really re-exposes the importance of an Exit Ticket…marking evidence of students' journey on their progress from conceptual understanding to procedural fluency. Next, John Stevens and Matt Audrey inspire dozens to take a risk to give choice in students as to how they can demonstrate their understanding…and procedural fluency. Michael Fenton lays out a case to vary the verbs in what we ask kids to do, with a general sequence of asking them to observe, estimate, sketch graphs, explain, interpret and then become increasingly more formal and precise, but only AFTER students' reasoning and ideas are out. Bill McCallum clearly emphasized that at the lesson and unit levels, there is a great need to move from informal thinking and reasoning, over time, to the more formal, abstract and procedurally fluent ways of thinking. Andrew Stadel then goes right at it…and exposes the powerful Math Teaching Practice #6 from Principles to Actions (#nctmp2a) stating procedural fluency happens after conceptual understanding, using estimation, number lines, and clotheslinemath to illuminate that this transition happens "over time". For the grand finale, Dan Meyer takes the stage…repeatedly emphasizes the need to for us to help students develop the intellectual need for the conventions, procedures and skills that we want kids to have…moving them from very informal and conceptual ideas, to reason that these things (variables, arrays, grids, parentheses) actually help us, not give us more work to do. Concluding that we should be letting kids discover why we have these by briefly experiencing what mathematical life is like without them…HARDER, and do so before using them. Please take a moment to reflect on my take-aways above, and try to connect them to the chart below from Principles to Actions. Then think about where you are, the teachers you work with are, and how we can keep the momentum moving. CALL TO ACTION I propose that we now have many believers in the power and importance of conceptual understanding (first) as a foundation for procedural fluency, but now is the time for us all to dig deep into the intricate “how” to make that the reality using Principles to Actions and the Standards for Mathematical Practice as our foundation. Then, let's talk some more. In Talking Points style, do you agree, disagree, or are you unsure...and why?
32 Comments
** The reflection questions in italics below are welcomed to be used not only for yourself as a learner, but in facilitating the professional learning of others. ** When was the last time you were engaged in productive struggle while working on a mathematical task? (long pause…not a rhetorical question). When was the last time you were engaged in un-productive struggle? (another long pause…really, think about it) At NCSM 2016, Tim McCaffrey, Jill Bueckling and I decided to collaboratively work on deepening our high school content knowledge through Making Sense of Teaching Math for High School. Despite our geographic differences, we set a schedule for how much we would read and wanted to give the video-conference app Zoom (as recommended by Mike Flynn) a whirl on occasion. We all humbly approached with a growth mindset, knowing that we’ve all been taught in ways that did not encourage reasoning and problem-solving as high school students ourselves, and were working our own mathematical depth. We are absolutely loving the book. If you’re an elementary or middle school teacher, and are interested in knowing where your content standards are headed, and what some of the big ideas to emphasize in your own classroom are, this is an excellent resource to try to piece some of that together. If you’re a high school teacher who understands the content, but could maybe use something to fill in the gaps as to how different concepts connect, this one is for you, too! If you’re somebody who would like to see high school students reasoning and problem-solving in live video…well, they’ve got that covered, too. Feel free to head on over to #MSMTHS and join the conversation, which includes the authors Juli Dixon, Ed Nolan, and Farshid Safi, as well as some promotional support by Solution Tree. In doing some of the tasks presented in the book independently so far, I’ve engaged in some productive (and un-productive) struggle. For example, in the Geometry chapter I was working on the task below. I noticed myself initially productively struggling. In other words, I was trying to make sense of the problem, testing out different ideas, drawing visual representations to match the context, conjecturing, looking for structure…sound like the Standards for Mathematical Practice?
Could it be that the threshold between productive and un-productive struggle lies in the Standards for Mathematical Practice? Is there a proportional relationship between the magnitude of engagement in the SMP’s and the magnitude of productive struggle? However, my productive struggle became unproductive when I felt I had exhausted all of my options. As I tried to reach deep down into my own conceptual understandings, I had nothing else to pull from. How often do your students get to this point? How often do your students reach down into their own conceptual understandings, and feel they’ve exhausted all of their options? What’s your role as the teacher in this situation? How does your understanding of progressions of mathematical content come into play when students shift from productive struggle to un-productive struggle? I found myself reflecting in that moment on what it’s like to be a student and not knowing where to go or what to do. Often, what students are told/asked in this moment include the following… “What did you do first? What do you think you should do next?” “Why don’t you try a different strategy?” “Go back in and read the problem again.” “Keep trying. You’ll get it.” “Turn back to your notes and see what it says.” None of these prompts would have helped me transition out of my unproductive struggle back into productive struggle. In this moment… I wanted to hear somebody else’s thinking as they’re concurrently working on the task. I wanted to see how others working on the task are representing the context. I wanted to know that others, just like me, are struggling, too. I wanted to hear what others are struggling with, what they’re thinking might work and why. I wanted others’ thinking to be visible. THESE ARE TEACHER ACTIONS THAT WOULD MOVE ME FROM UN-PRODUCTIVE TO PRODUCTIVE STRUGGLE. I would’ve felt less capable and/or outright defeated if somebody who already deeply understood the content in the task was telling me where I’m going wrong, or what to do next. If that same person suggested trying another strategy, my response would have been simple. “I don’t have any other strategies to try.” So what’s the point? If I were a student sitting at my desk, trying to make sense, reason abstractly, look for and make use of structure and so on, and if I’m restricted from having social interaction where other students’ thinking (NOT the teachers’ thinking) is visible, my struggle remains un-productive. The mathematics lies in other students’ thinking, as we are all working on a common task…struggling together in many different ways. Our struggles become shared understandings, but only if they’re shared. Tomorrow, I video-conference with 2 math friends on Zoom, where we will make each others’ thinking visible around a task that promotes reasoning and problem-solving by engaging in meaningful discourse, using and connecting each others’ representations and building conceptual understanding as a foundation for greater procedural fluency. We will grapple together, talking and trying to make sense of each others’ thinking through discourse and each others’ representations. However, if I’m not allowed to talk to my peers, see and hear what they’re thinking, and/or connect their representations to my own, then math is something that does not make sense…and it’s just for other people. I’ll just sit, and wait for somebody to show me what to do, if I do anything at all. The Challenge Please substitute my own thoughts as I was struggling un-productively out of the text above and insert some of your students’ names. Math is social. When we take away access for students to see each others’ thinking, we take away access to the mathematics. This access comes through opportunities for students to make their own and each others’ thinking visible in the form of meaningful discourse and making sense of other students’ representations of mathematical situations. We often get the question from teachers, parents, administrators, and just about any other type of adult…what do we do about kids who are “behind”? Everybody wants a nice clean answer, but it's incredibly rare to hear one. In the past few months, Kristian Quiocho, Shannon Andrews, Chris Perez and I have paired in different combinations to plan and facilitate several full-day task-based workshops on different progressions of some of the content domains. For example, we spent a day with teachers on the OA domain, another day on the K-5 Geometry domain, another on Mathematical Modeling, and another on the Ratios and Proportional Relationships domain – all focused on how the content progresses over time. All of the slides for each of those sessions are in the Workshop Resources page of this website. In each of those sessions we started with a task that draws out some of the big ideas that we identified in the Progressions Document for that domain. Teachers struggled through the task at varying levels, independently then collaboratively. As always, we used a 5 Practices model to capture some of the teachers' representations, sequenced them, and displayed them 1 or 2 at a time, asking teachers to interpret the representations, to make connections amongst those representations (alike/different), and of course asked questions to connect those representations to the big mathematical ideas that are occurring in them. Critical distinction… when using the 5 Practices model, we can’t emphasize enough the value in having the creator of the representation to NOT present or talk about their own representation in the “connect” phase, unless absolutely necessary. It’s critical to give teachers (and kids) time to do an informal notice/wonder about each representation that’s displayed, and have an opportunity to engage in discourse with a peer about what they believe the representation is showing, and what the author of that representation was thinking (SMP 1, 2, 6, and 7). Below are 3 of the representations that we asked teachers to connect from the Penguin task in the Operations and Algebraic Thinking session. What's similar? What's different? What big mathematical ideas exist in all of them? After teachers grappled with the first task, we asked them to generalize the different ways of thinking that they just engaged in and massage the language while keeping it informal. Below is a sample from the Ratios and Proportional Reasoning session that the teachers identified as big ideas that emerged in the first task. Here’s where it gets intense…we had an almost equal distribution of teachers from elementary, middle and high school in the Ratios and Proportional Relationships session, even though this was technically middle school content. Do you have, or know teachers that have, a class of students with wide variety of “content knowledge” in the classroom…varying levels of proficiencies? Kids that are all over the place, almost all of the time?
Teachers then went into their grade level standards chapter of the CA Math Framework (the Progressions Documents would work if you’re not in CA, or if using another state’s document is unappealing to you) and looked for the same way of thinking from the chart in the content of their grade level. Amazing conversations ensued in the whole group discussion afterwards. Then Jamie Duncan drops a bomb noticing that the “for every __, there is __” way of thinking shows up in her 1st Grade Measurement standards…think about it! Wait...think more about it. Heads spinning in the room, a Trigonometry teacher who the bow on noticing the same way of thinking shows up in developing Trig Ratios...heads spinning faster. Are you tired of going to committee meetings that are not focused on anything helpful? Ever been to a “Vertical Articulation Meeting” that’s a complete waste of time? What would happen if these meetings were focused on making explicit connections to a domain, where the mathematics was the agenda and context for all of the conversation, and the big mathematical ideas got exposed across grade levels and grade spans? The rest of the day we spent doing more tasks and refining our language of the Big Ideas that underlie the domain, becoming more formally aligned to the language of the Progressions Documents, and an understanding of what those words mean in the context of a classroom. (As an example, what does the OA Progressions Document mean when it presses on “extending arithmetic beyond whole numbers”?) The collaboration and deepened content knowledge in these sessions have been just plain awesome…but not the point for this post. So what is the point? What’s the connection between giving teachers in-depth experiences into mathematical content, learning about how the mathematics progresses across grades and grade span and the question “what do we do about the kids who are behind?” I have my own ideas, but if you made it this far into the post, you probably have better ones than me. So let’s hear it… |
Learn from each other
Please read and respond so we can build shared understandings. Archives
November 2016
Categories |




 RSS Feed
RSS Feed
